BANGUN SEGI n,k BERATURAN
Oleh : Budi Permana, S.Si
Lomba Karya Ilmiah Matematika
Pada tahun 1987, Himpunan Mahasiswa Matematika (HIMATIKA) ITS menyebarkan poster tentang Lomba Karya Ilmiah Matematika ke sekolah-sekolah menengah atas di seluruh Indonesia. Dalam selebaran poster tersebut, dinyatakan bahwa lomba penulisan karya ilmiah matematika memiliki topik dan tema yang cukup luas, sehingga para peserta diberikan keleluasaan dalam menyusun karya tulis.
Pada hari ketika selebaran itu dipasang, saya terinspirasi untuk mengikutsertakan karya tulis saya yang telah saya rintis sejak kelas 1. Saya yakin, karya tulis saya sesuai dengan persyaratan yang dicantumkan.
Saya pun mulai menyusun ulang apa yang pernah saya tampilkan di majalah dinding sekolah. Lembar demi lembar akhirnya terkumpul, terdiri dari semua tulisan yang pernah saya buat. Kemudian, saya menyusun daftar isi baru yang disesuaikan dengan metode penulisan lomba karya ilmiah matematika.
Akhirnya, saya memutuskan untuk memberi judul naskah tersebut: “Merintis Eksistensi Bangun Segi 2,5 Beraturan.” Saya sengaja memilih judul ini agar pembaca tertarik membacanya hanya dari judulnya. Dengan menyebut "bangun segi 2,5 (dua setengah) beraturan", pembaca akan penasaran dan berpikir keras seperti apa bentuknya? Dengan begitu, mereka akan membaca lebih saksama, sambil ingin tahu bagaimana bentuk fisiknya.
Awal Ide Penulisan di Kelompok Ilmah Remaja SMAN 2 Banyuwangi
Saat kelas 1 di SMAN 2 Banyuwangi, saya mendaftar sebagai anggota Kelompok Ilmiah Remaja (KIR) SMAN 2 Banyuwangi, yang dikenal dengan nama Karisma2. Pada awal keanggotaan, seluruh anggota diminta membuat karya tulis. Saat itu, saya mendapat ide untuk menulis tentang cara menghitung luas bangun segi sejuta beraturan.
Gagasan ini sudah mulai terngiang-ngiang dalam benak saya sejak mengenal aturan trigonometri sinus, kosinus, dan tangen. Awalnya hanya sekadar iseng menghitung luas berbagai bangun, hingga akhirnya saya menyadari bahwa saya berhasil menemukan rumus untuk menghitung luas bangun segi-n beraturan.
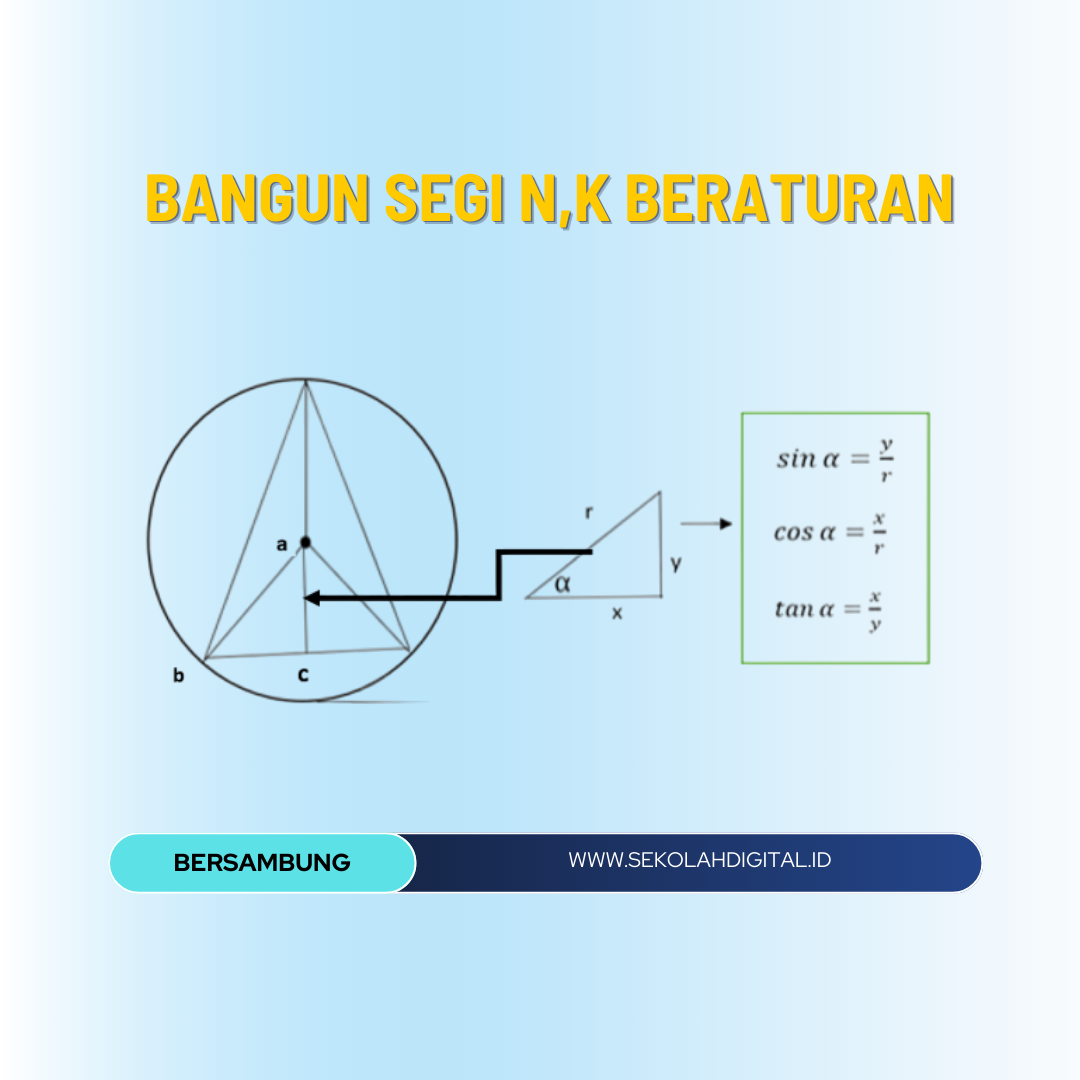
Logika berpikir saya dimulai dari bangun segitiga beraturan yang terbentuk dari tiga buah segitiga sama sisi.
Kemudian saya cari luas masing-masing segitiga tersebut. Rumus pertama berdasarkan panjang sisi, rumus kedua berdasarkan jari-jari. Saya menggunakan definisi sinus, cosinus, dan tangen yang melekat pada bangun segitiga.
1. LUAS BANGUN BERDASARKAN JARI-JARI
Oleh karena banyaknya segitiga dalam suatu bangun segi n adalah n buah, maka luasnya adalah n x L segitiga abc. Jadi, luas bangun segi n beraturan adalah
Ini adalah luas bangun segi n beraturan berdasarkan jari-jari (r).
2. LUAS BANGUN BERDASARKAN PANJANG SISI
Oleh karena banyaknya segitiga dalam suatu bangun segi n beraturan adalah n buah, maka luasnya adalah n x L segitiga abc. Jadi, luas bangun segi n beraturan adalah
Ini adalah luas bangun segi n beraturan berdasarkan panjang sisi.
Rumus sudut luar bangun segi n beraturan adalah
3. RUMUS LENGKAP LUAS BANGUN SEGI n BERATURAN
- Rumus luas bangun segi n beraturan berdasarkan panjang jari-jari
- Rumus luas bangun segi n beraturan berdasarkan panjang sisi
- 3. Kita coba menghitung luas segi 4 beraturan, berarti n = 4. Jadi, luasnya adalah:
Perhitungan di atas membuktikan bahwa rumus yang digunakan dapat menghasilkan nilai luas yang benar untuk bangun datar beraturan. Ketika diuji pada segi empat beraturan, hasilnya sesuai dengan rumus dasar yang sudah dikenal, yaitu Luas= s2. Dengan demikian, rumus ini terbukti valid dan dapat digunakan untuk menghitung luas berbagai bangun segi-n beraturan secara umum.